链表(linked list)是一种常见的线性数据结构。常见的链表分类有:单向链表,双向链表,循环链表,静态链表等。
链表节点结构
链表结构又分为带头结构的链表与不带头结构的链表。
单向链表
1 | struct Node { |
2 | int data; |
3 | struct Node *next; |
4 | } |
5 | /* 链表头,可带可不带 */ |
6 | struct Header { |
7 | int length; |
8 | struct Node *next; |
9 | }; |
10 | |
11 | typedef struct Node Node; |
12 | typedef struct Header pHead; |
双向链表
1 | struct Node; |
2 | typedef struct Header* pHead; |
3 | typedef struct Node* pNode; |
4 | |
5 | struct Header{ |
6 | int length; |
7 | pNode next; |
8 | }; |
9 | |
10 | struct Node{ |
11 | int data; |
12 | pNode pre; |
13 | pNode next; |
14 | }; |
循环链表与单向链表或双向链表结构相同,只是尾指针不指向NULL,而是指向头节点。
链表的基础操作
插入
双向链表的插入
1 | pNode->next = pCur->next; |
2 | pCur->next->pre = pNode; |
3 | pNode->pre = pCur; |
4 | pCur->next = pNode; |
删除
1 | pPre = pDelete->pre; |
2 | pNext = pDelete->next; |
3 | pPre->next = pNext; |
4 | pNext->pre = pPre; |
链表的常见考点
反转链表
迭代反转链表
1 | node* ReverseList(node* pHead){ |
2 | node* pTemp = pHead; |
3 | node* pReverse = NULL; |
4 | |
5 | if(pHead == NULL || pHead->_next == NULL) |
6 | return pHead; |
7 | |
8 | while(pTemp != NULL){ |
9 | node* pNextNode = pTemp->_next; |
10 | pTemp->_next = pReverse; |
11 | pPreverse = pTemp; |
12 | pTemp = pNextNode; |
13 | } |
14 | |
15 | return pReverse; |
16 | } |
在迭代链表中:
pTemp指针用于遍历要反转的链表。pNextNode临时保存pTemp->_next指针。pReverse指向反转后链表的头指针。
递归反转链表
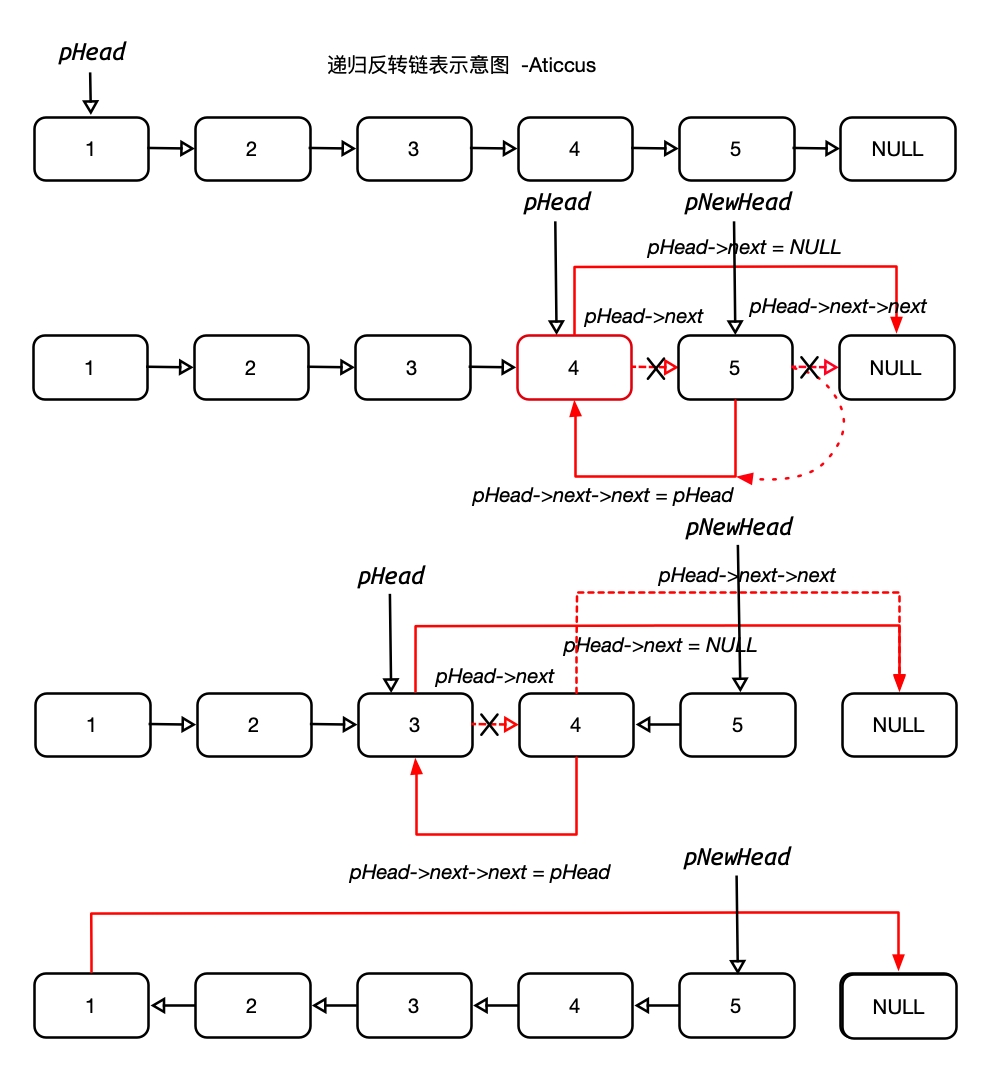
1 | node* ReverseList_DG(node* pHead){ |
2 | node* pNewHead = NULL; |
3 | |
4 | if(pHead == NULL || pHead->_next == NULL) |
5 | return pHead; |
6 | |
7 | pNewHead = ReverseList_DG(pHead->_next); |
8 | |
9 | pHead->_next->_next = pHead; |
10 | pHead->_next = NULL; |
11 | |
12 | return pNewHead; |
13 | } |
合并有序链表
LeetCode 21.合并两个有序链表
将两个升序链表合并为一个新的升序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
1 | 输入:1->2->4, 1->3->4 |
2 | 输出:1->1->2->3->4->4 |
非递归解法
1 | /** |
2 | * Definition for singly-linked list. |
3 | * struct ListNode { |
4 | * int val; |
5 | * struct ListNode *next; |
6 | * }; |
7 | */ |
8 | struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2){ |
9 | struct ListNode *begin = malloc(sizeof(struct ListNode)); |
10 | struct ListNode *tmp_p = begin; |
11 | struct ListNode *l1_p = l1; |
12 | struct ListNode *l2_p = l2; |
13 | while(l1_p != NULL || l2_p != NULL){ |
14 | struct ListNode *a = malloc(sizeof(struct ListNode)); |
15 | tmp_p->next = a; |
16 | if(l1_p == NULL){ |
17 | a->val = l2_p->val; |
18 | tmp_p = a; |
19 | l2_p = l2_p->next; |
20 | }else if(l2_p == NULL){ |
21 | a->val = l1_p->val; |
22 | tmp_p = a; |
23 | l1_p = l1_p->next; |
24 | }else{ |
25 | if(l1_p->val > l2_p->val){ |
26 | a->val = l2_p->val; |
27 | tmp_p = a; |
28 | l2_p = l2_p->next; |
29 | }else{ |
30 | a->val = l1_p->val; |
31 | tmp_p = a; |
32 | l1_p = l1_p->next; |
33 | } |
34 | } |
35 | } |
36 | tmp_p->next = NULL; |
37 | |
38 | return begin->next; |
39 | } |
递归解法
1 | struct ListNode* mergeTwoLists(struct ListNode* l1, struct ListNode* l2) { |
2 | if (l1 == NULL) { |
3 | return l2; |
4 | } |
5 | else if (l2 == NULL) { |
6 | return l1; |
7 | } |
8 | |
9 | if(l1->val < l2->val){ |
10 | l1->next = mergeTwoLists(l1->next,l2); |
11 | return l1; |
12 | }else{ |
13 | l2->next = mergeTwoLists(l1,l2->next); |
14 | return l2; |
15 | } |
16 | } |
查找中间节点
1 | node* SearchMidNode(node* pHead){ |
2 | node* pFast = pHead; |
3 | node* pSlow = pHead; |
4 | |
5 | if(pHead == NULL || pHead->_next == NULL) |
6 | return NULL; |
7 | |
8 | while(pFast != NULL && pFast->_next != NULL){ |
9 | pSlow = pSlow->_next; |
10 | pFast = pFast->_next->_next; |
11 | } |
12 | |
13 | return pSlow; |
14 | } |
查找倒数第K个节点
1 | node* FindLastKNode(node* pHead, int key){ |
2 | node* pSlow = pHead; |
3 | node* pFast = pHead; |
4 | |
5 | if(pHead == NULL) |
6 | return NULL; |
7 | |
8 | while(key--){ |
9 | if(pFast == NULL) |
10 | return NULL; |
11 | pFast = pFast->_next; |
12 | } |
13 | |
14 | while(pFast != NULL){ |
15 | pFast = pFast->_next; |
16 | pSlow = pSlow->_next; |
17 | } |
18 | |
19 | return pSlow; |
20 | } |
链表是否有环
1 | node * isHaveCircle(node* pHead){ |
2 | node* pFast = pHead; |
3 | node* pSlow = pHead; |
4 | |
5 | if(pHead == NULL) |
6 | return NULL; |
7 | |
8 | while(pFast != pSlow && pFast->_next != NULL){ |
9 | pFast = pFast->_next->_next; |
10 | pSlow = pSlow->_next; |
11 | } |
12 | |
13 | if(pFast->_next == NULL){ |
14 | return NULL; |
15 | } |
16 | |
17 | return pSlow; |
18 | } |
求环的入口节点
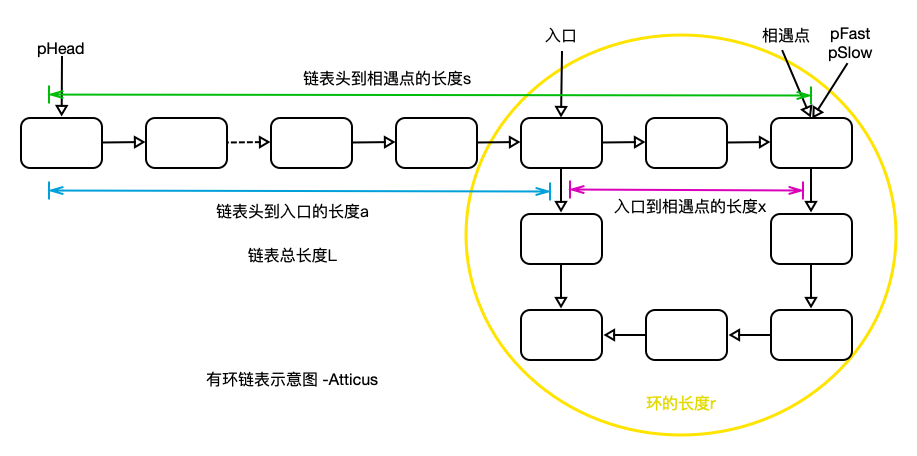
如图所示,当快慢指针相遇时,slow还没走完链表,fast指针已经在环内循环链n圈。假设slow指针走了s步,即链表头距相遇点为s,那么fast指针走链2s步,fast指针走过的长度还等于s+n*r,r为环的长度。则:
$$ 2 \ast s = s+n \ast r => s=n \ast r $$
假设整个链表长度为L,入口到相遇点的距离为x,起到到入口的距离为a,则有:$$ a+x=s=n \ast r $$ $$ a+x=(n-1) \ast r+r=(n-1) \ast r+(L-a) $$ $$ a=(n-1) \ast r+(L-a-x) $$
所以:在使用两个指针,从链表头与相遇点再次出发,两指针相遇点也就是链表环入口。
1 | node* GetCircleIntoNode(node* pHead){ |
2 | node* pBeginNode = pHead; |
3 | node* pMeetNode = NULL; |
4 | |
5 | pMeetNode = isHaveCircle(pHead); |
6 | if(!pMeetNode){ |
7 | return NULL; |
8 | } |
9 | |
10 | while(pBeginNode != pMeetNode){ |
11 | pBeginNode = pBeginNode->_next; |
12 | pMeetNOde = pMeetNode->_next; |
13 | } |
14 | |
15 | return pMeetNode; |
16 | } |
求环的长度
1 | int GetCircleLength(node* pHead){ |
2 | size_t len = 0; |
3 | node* pMeetNode = NULL; |
4 | node* pCur = NULL; |
5 | |
6 | if((pMeetNode = isHaveCircle(pHead)) == NULL) |
7 | return 0; |
8 | |
9 | pCur = pMeetNode->_next; |
10 | |
11 | while(pCur != pMeetNode){ |
12 | len++; |
13 | pCur = pCur->_next; |
14 | } |
15 | |
16 | return len; |
17 | } |
求有环链表的长度
链表长度L = 起点到入口点的距离a + 环的长度r 。
静态链表
在此不展开讲,放两篇文章:
