图(graph)由顶点(vertex)与边(edge)的构成，研究元素间多对多的关系。

图由顶点(vertex)与边(edge)组成。由一条边链接的两个顶点互为邻接点。若边有方向则此时的图为有向图，连接图的边无方向则为无向图。

若一个无向图中每两个顶点之间都存在一条边，则称这个无向图为完全无向图。完全无向图中若顶点数为n，则边数为n(n-1)/2。

若一个有向图中每两个顶点都存在方向相反的两个边，则称该图为完全有向图。完全有向图中顶点数为n,边数为n(n-1)。

某个顶点的边数称为顶点的度(degree)。有向图中度又分为出度与入度，出度与入度的和为该顶点的度。

图的边数很多接近完全图的称为稠密图，边数很少的称为稀疏图。

与边有关的数据信息称为权(weight)，边上带权值的图称为网图或网络。

路径长度指一条路径上经过的边的数目。

在无向图中，若两顶点之间有路径，则称者两顶点是连通的。若无向图中任意两个顶点之间都连通，则称为连通图。如果不是连通图，则图中极大连通子图称为连通分量。连通图只有一个连通分量，即它本身，非连通图不止一个连通分量。

在有向图中，若任意两个顶点之间都有双向的路径，则称之歌有向图为强连通图。有向图的极大连通子图称为强连通分量。

图的存储结构

邻接矩阵

邻接矩阵存储法用一个一维数组存储图中的顶点信息，一个二维数组存储顶点关系，即边的信息。

无向图需要对称赋值，有向图不需要对称赋值。

1
#define MAX_VERTEX_NUM 100
2
typedef struct{
3
  int n;  /* 图中顶点数目 */
4
  int e;  /* 图中边的数目 */
5
  
6
  int vexs[MAX_VERTEX_NUM]; /* 顶点存储 */
7
  int deges[MAX_VERTEX_NUM][MAX_VERTEN_NUM]; /* 边存储 */
8
}Graph;

邻接表

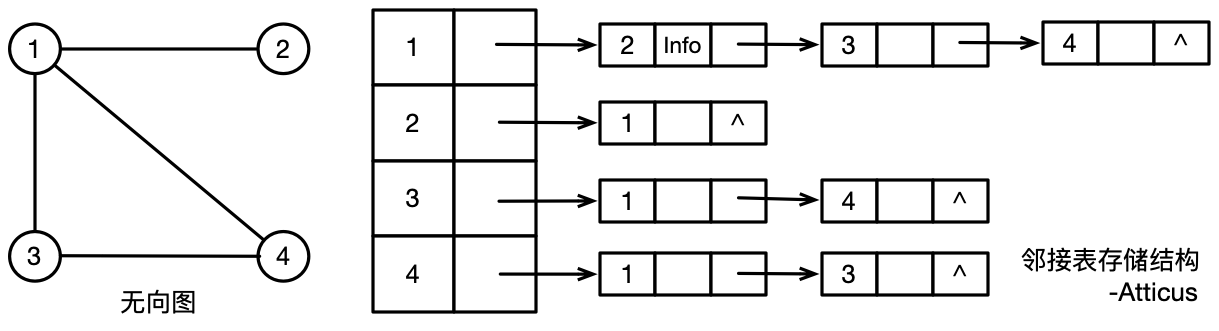
邻接表存储结构

邻接表用于有向图存储时，邻接表每个顶点的边结点个数反应来该顶点的出度，但是要获取有向图的入度，需要遍历整个邻接表。反之以终点节点作为顶点建立邻接表可以容易获取入度。

1
#define MAX_VERTEX_NUM 100
2
typedef struct EdgeNode{
3
  int adjvex;	/* 邻接点域，存储该顶点邻接点 */
4
  int weight;	/* info数据域，存储权值，非网图可省略 */
5
  struct EdgeNode* next; /* 指向顶点的下一个邻接点 */
6
}EdgeNode;  /* 边结点 */
7
8
typedef struct VertexNode{ /* 顶点结构 */
9
  int data;	/* 存储顶点信息 */
10
  EdgeNode* firstedge;	/* 指向该顶点相邻的其他顶点 */
11
}VertexNode,AdjList[MAX_VERTEX_NUM];
12
13
typedef struct{
14
  AdjList adjList;
15
  int n;	/* 图中顶点的数目 */
16
  int e;	/* 图中边的数目 */
17
}GraphAdjList;

十字链表

十字链表结构在邻接表结构的基础上加入来指向弧尾的指针，是一种针对有向图的存储结构。

1
#define MAX_VERTEX_NUM 100
2
typedef struct EdgeNode{
3
  int headvex;	/* 有向图中弧头指向的顶点编号 */
4
  int tailvex;	/* 有向图中弧尾指向的顶点编号 */
5
  struct EdgeNode* tlink, *hlink; /* 指向以该顶点为弧尾，弧头的指针 */
6
  int info;  /* 弧权信息 */
7
}EdgeNode;  /* 边结构 */
8
9
typedef struct{
10
  int data;
11
  EdgeNode* firstin, *firstout; /* 该顶点的第一个弧入，弧出指针 */
12
}VertexNode, GList[MAX_VERTEX_NUM];  /* 顶点结构 */
13
14
typedef struct{
15
  GList list;
16
  int n;
17
  int e;
18
}CGraph;

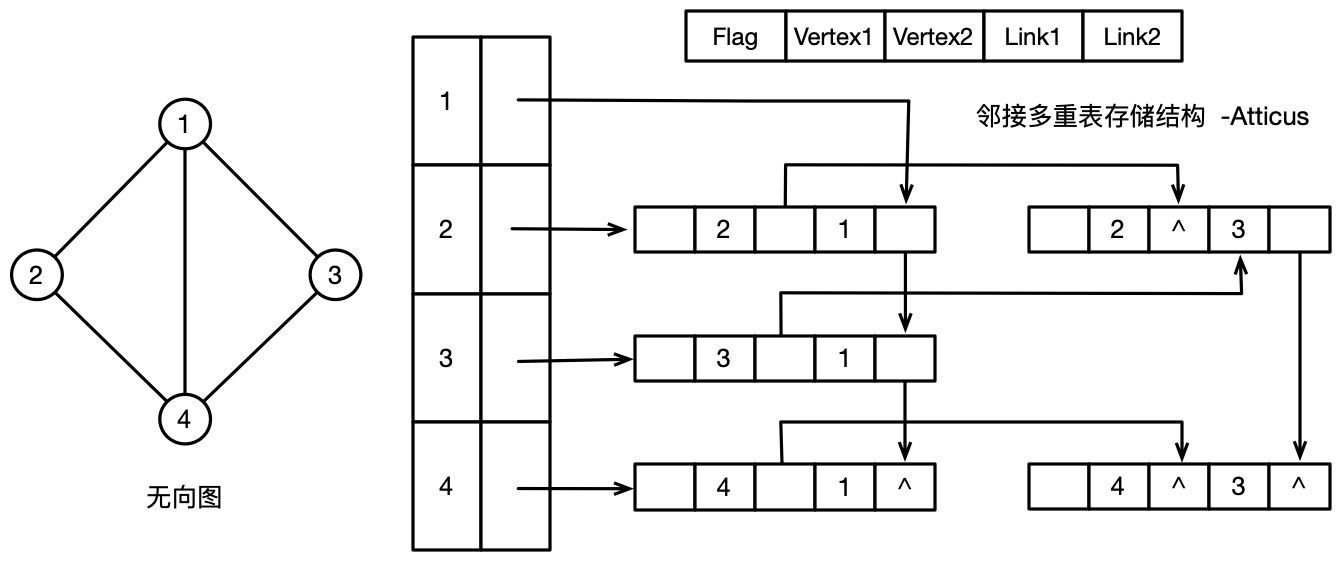
邻接多重表

邻接多重表也是一种针对无向图的存储结构，邻接表标示的无向图中相同的表结点存储在两个链表中。若要对无向图中的边进行操作，需要对两个链表中表示同一个相同的表结点进行相同的操作。

邻接多重表使用一个表结点存储邻接表中的两个结点。

邻接多重表存储结构

1
#define MAX_VERTEX_NUM 200
2
typedef struct EdgeNode{
3
  union{
4
    int visited;
5
    int unvisited;
6
  }flag;
7
  int vexi;	/* 一个边的两个顶点 */
8
  int vexj;
9
  struct EdgeNode* ilink; 	/* 分别指向依附这两个顶点的下一条边 */
10
  struct EdgeNode* jlink;
11
  int info;	/* 与边相关的信息 */
12
}EdgeNode;  /* 边结构 */
13
14
typedef struct VertexNode{
15
  int data;
16
  EdgeNode *firstedge;
17
}VertexNode;
18
19
typedef struct{
20
  VertexNode adjmulist[MAX_VERTEX_NUM];
21
  int n;
22
  int e;
23
}AMLGraph;

图的遍历

深度优先遍历

深度优先遍历(Depth First Search,DFS)是树的先序遍历的推广。在树的4种遍历方法中可以根据不同的方法确定唯一的路径。但是在图中顶点的顺序是任意的，到达每个顶点的路径可能有多条，并且图中可能存在回路，在遍历的过程中一个顶点可能被重复访问多次。

所以在DFS遍历图中需要设定两个辅助变量:

  1. 状态数组 visited[]。该数组用来记录每个顶点的被访问状态。
  2. 记录当前访问位置的栈 stack[]。每访问一个顶点，就让该顶点入栈，若遇到一个顶点，该顶点不存在未被访问的邻接点，则从栈中弹出该顶点。

基于邻接矩阵存储的深度优先递归算法

1
int visited[MAX_VERTEX_NUM] = {0};
2
void DFS(Graph G, int i){
3
  int j;
4
  visited[i] = 1;  /* 当前访问顶点状态改为1以访问 */
5
  printf("%d",G.vexs[i]);
6
  for(j = 0; j < G.n; j++){
7
    if(G.edges[i][j] == 1 && visited[j] == 0){
8
      DFS(G,j);
9
    }
10
  }
11
}

基于邻接表存储的深度优先递归算法

1
int visited[MAX_VERTEX_NUM] = {0};
2
void DFS(GraphAdjList GL, int i){
3
  EdgeNode *p;
4
  visited[i] = 1;
5
  printf("%d",GL.adjList[i].data);
6
  p = GL.adjList[i].firstedge;
7
  while(p){
8
    if(!visited[p->adjvex])
9
      DFS(GL, p->adjvex);
10
    p=p->next;
11
  }
12
}
13
``` 
14
### **广度优先遍历**
15
广度优先遍历(Breadth First Search,BFS)类似于树的按层遍历。基本思想为：任意选对一个顶点v开始本次访问，访问v之后依次访问v的待访问邻接点，并将以访问的顶点放入队列Q中。按照Q中顶点的次序，依次访问这些已被访问过的顶点的邻接点。如果队头的顶点不存在待访问的邻接点，则让队头出队，访问新队头的待访问邻接点，直到队列为空。
16
17
基于邻接矩阵的广度优先遍历
18
```c
19
void BFS(Graph G){
20
  int i,j;
21
  SeqQueue Q = Create();
22
  for(i = 0; i < G.n; i++)
23
    visited[i] = 0;
24
  for(i = 0; i < G.n; i++){
25
    if(visited[i] == 0){
26
      visited[i] = 1;
27
      printf("%d",G.vexs[i]);
28
      Insert(&Q, i);  /* 入队 */
29
      while(!IsEmpty(Q)){
30
        Del(Q);  /* 出队 */
31
        for(j = 0; j < G.n; j++){
32
          if(G.edges[i][j] == 1 && visited[j] == 0){
33
            visited[j] = 1;
34
            printf("%d",G.vexs[j]);
35
            Insert(&Q, j); /* 入队 */
36
          }
37
        }
38
      }
39
    }
40
  }
41
}

基于邻接表的广度优先遍历

1
void BFS(GraphAdjList GL){
2
  int i;
3
  EdgeNode *p;
4
  SeqQueue Q = Create();
5
  for(i = 0; i < GL.n; i++)
6
    visited[i] = 0;
7
  for(i = 0; i < GL.n; i++){
8
    if(!visited[i]){
9
      visited[i] = 1;
10
      printf("%d",GL.adjList[i].data);
11
      Insert(&Q, i);
12
      while(!IsEmpty(Q)){
13
        Del(Q);
14
        p = GL.adjList[i].firstedge;
15
        while(p)
16
        {
17
          if(visited[p->adjvex] == 0){
18
            visited[p->adjvex] = 1;
19
            printf("%d",GL.adjList[p->adjvex].data);
20
            Insert(&Q, p->adjvex);
21
          }
22
          p = p->next;
23
        }
24
      }
25
    }
26
  }
27
}

上述的遍历仅针对一个连通分量或者说一个连通图的遍历算法，要实现非连通图的遍历，需要一个简单的函数对DFS或者BFS算法调用。

1
void connected(Graph G){
2
  int i;
3
  for(i = 0; i < G.n; i++){
4
    if(visited[i] == 0){
5
      DFS(G, i);
6
    }
7
  }
8
}

最小生成树

一个连通图的生成树，是包含来该连通图全部顶点的一个极小连通子图。顶点数目为n的连通图的生成树，必定具有n个顶点和n-1条边。不同的遍历算法会产生不同的生成树。

加权图生成树的代价是指该生成树所有边的权值之和。最小生成树就是指所有生成树中权值之和最小的那一颗或多棵。

Prim(普里姆)算法

Kruskal(克鲁斯卡尔)算法

最短路径

单源最短路径问题-Dijkstra(迪杰斯特拉)算法

任意两点之间最短路径-Floyd(弗洛伊德)算法

拓扑排序

关键路径