KMP算法是一种改进的字符串匹配算法, 由D.E.Knuth, J.H.Morris和V.R.Pratt提出, 无论是基于确定有限状态自动机机(Determinstic Finite Automata, DFA)的KMP实现还是基于部分匹配表(Parital Match Table, PMT)的KMP实现,其核心思想都是利用匹配失败后的信息,尽可能的减少模式串与主串的匹配次数以达到快速匹配的目的。

朴素模式(Brute-Force)匹配算法

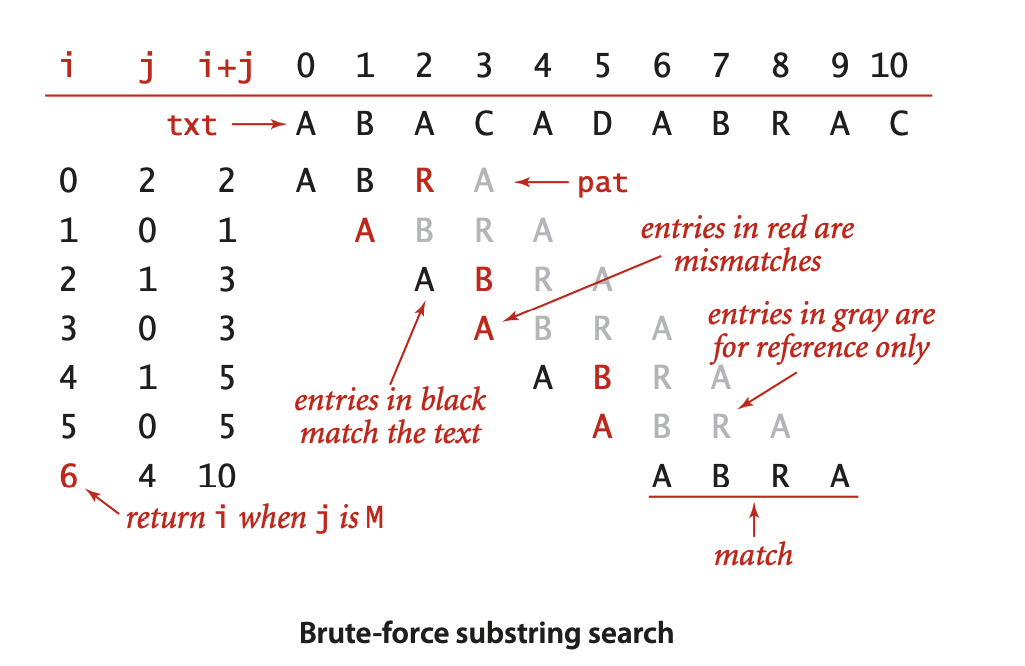
朴素的模式匹配算法又称为暴力匹配算法,即当遇到不相等时,回退从头开始逐个比较。

朴素的模式匹配算法

1
#include<stdio.h>
2
#include<string.h>
3
4
int find(char *txt, char *pat)
5
{
6
	int i = 0;
7
	int j = 0;
8
	while(i < strlen(txt) && j < strlen(pat)) /* strlen返回类型为无符号整形 */
9
	{
10
		if(txt[i] == pat[j]) /* 字符串相等,比较后续字符 */
11
		{
12
			i++;
13
			j++;
14
		}
15
		else /* 字符串不相等,j从头开始,i从下一个字符串开始 */
16
		{
17
			i = i - j + 1;
18
			j = 0;
19
		}
20
	}
21
22
	if(j == strlen(t))
23
		return i - j;
24
	else
25
		return -1;
26
}
27
28
int main()
29
{
30
	char *pat = "ABRA";
31
	char *txt = "ABACADABRAC";
32
33
	printf("%d\n", find(txt, pat));
34
	return 0;
35
}

主串txt的长度为n, 模式串pat的长度为m,则:

  1. 最好的情况是:一次匹配就命中,只比较了m次。
  2. 最坏的情况是:主串前n-m个位置都是在匹配了模式串pat的最后一个字符时才发现不匹配, 即这n-m个字符串都比较了m次,又因为串pat最后一次也比较了m次, 所以总比较次数为$(n-m)m+m = (n-m+1)m$, 算法复杂度为$O(nm)$。

基于DFA的KMP算法实现

确定有限状态自动机(DFA)

dfa

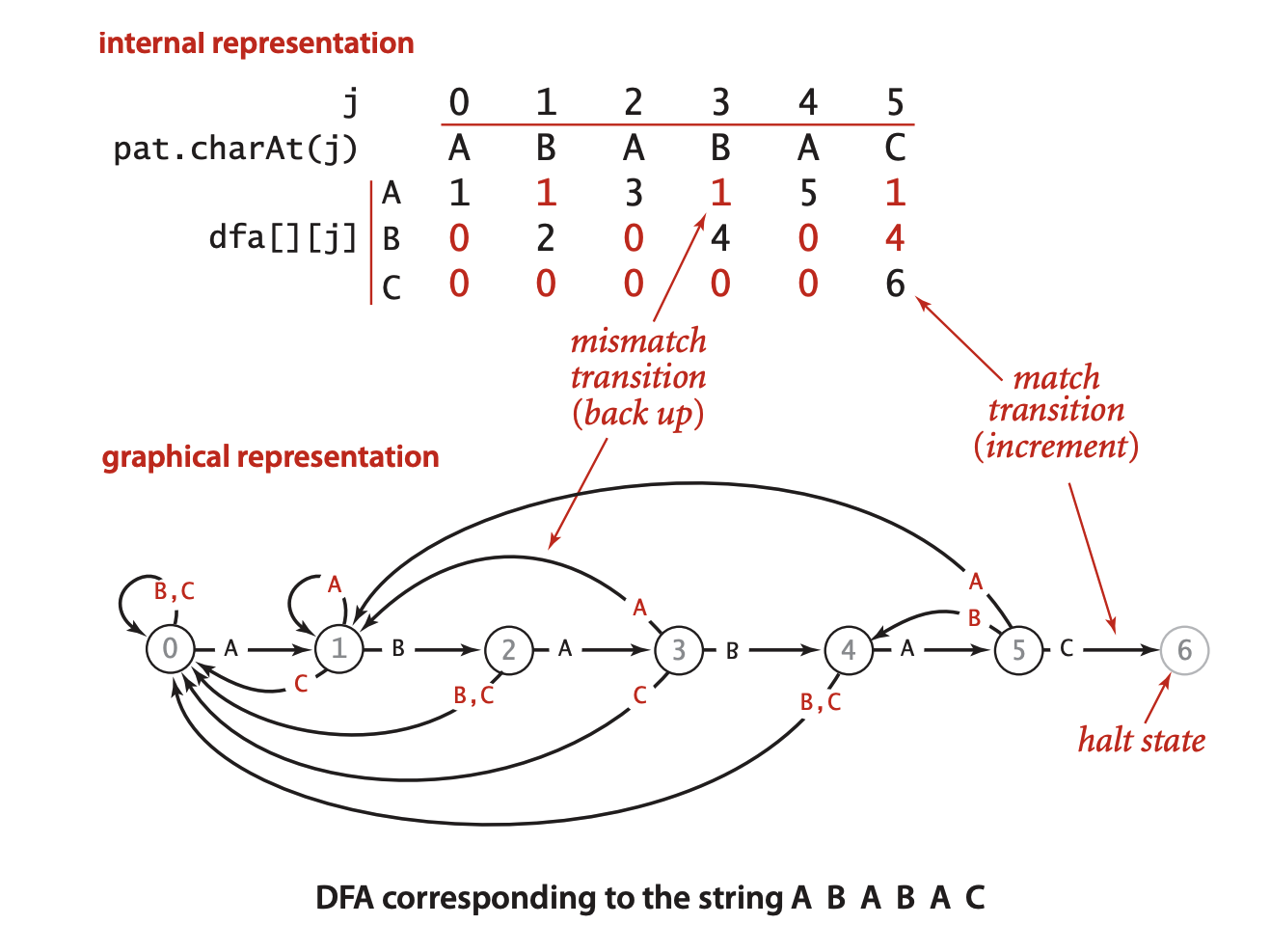
DFA由状态(数字标记的圆圈)和转换(带标签的箭头)组成。模式串中的每个字符都对应着一个状态,每个状态都能够转换为字母表中的任意字符。

在子字符串查找问题中(如上图所示): 每个状态都表示模式字符串中每个字符的索引值, 这些转换中只有一条是匹配转换(从j到j+1,箭头从左指向右), 其它的都是非匹配转换(箭头从右指向左)。

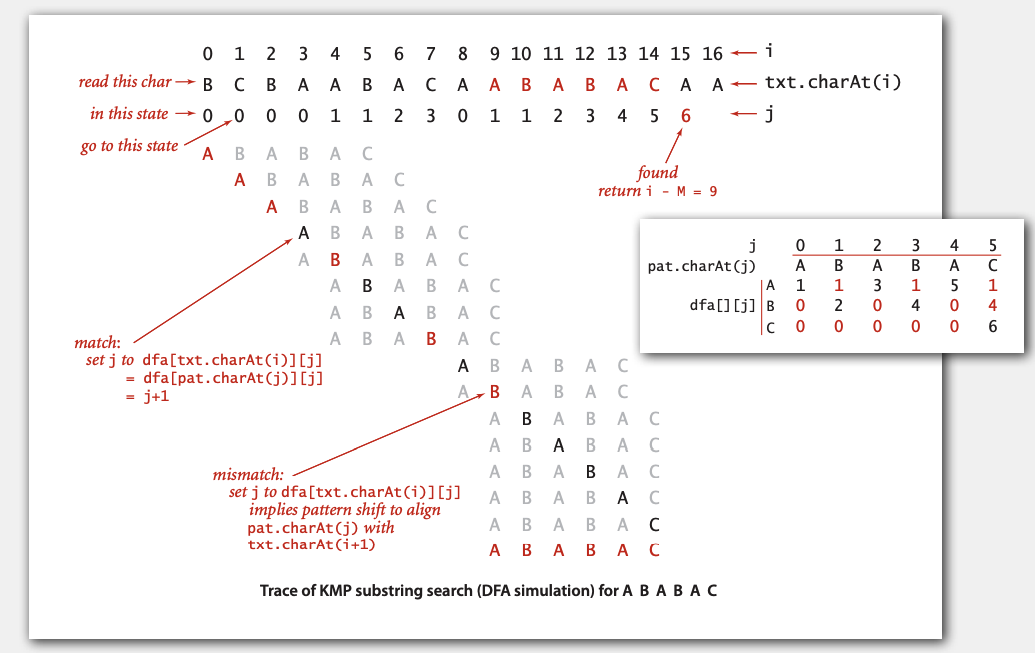
当我们在标记为j的状态中检查主串文本中的第i个字符时,自动机的处理过程为: 沿着转换dfa[txt[i]][j]前进并继续检查下一个字符(i+1)。对于一个匹配的转换,就向右移动一位, 因为dfa[pat[j]][j]的值总是j+1;对于一个非匹配转换,就向左移动。

自动机从状态0开始, 每次从左向右读取主串文本中的一个字符, 并移动到一个新状态, 如果自动机到达了停止状态M, 那么就在文本中找到了和模式串相匹配的一段子串(称这种状态为确定有限状态自动机识别了该模式), 如果在主串文本 扫描结束都未能达到状态M,就意味着主串中不存在该字符串。每个模式字符串都对应着一个自动机(dfa[][])。

dfa2

1
int search(char* txt)
2
{
3
	int i, j;
4
	int N = strlen(txt), M = strlen(pat);
5
6
	for(i = 0, j = 0; i < N && j < M; i++)
7
	{
8
		j = dfa[txt[i]][j];
9
	}
10
11
	if(j == M)
12
		return i - M;
13
	else
14
		return -1;
15
}

构造DFA

如何计算给定模式串的对应dfa[][]数组? 答案还是DFA本身!

在上一节朴素匹配模式中,当模式串pat[j]处不匹配时,j = 0 & i = i - j +1表示,模式串回退到头,文本串回退到本次匹配开始的的i的后一位。

当模式串pat[j]处不匹配时, 也意味着:pat[1]到pat[j-1]与对应的主串文本相匹配!!(这里从pat[1]而不是pat[0]开始是因为模式串pat要右移一位,与i = i - j + 1位置对齐)。

例如: 对于模式串ABABAC,当j = 5即pat[j] = 'c'时匹配失败时,按照上一节朴素匹配模式, 完全回退后重新匹配, 还会到达BABA状态3,因此可以将dfa[][3]复制到dfa[][5]并将C所对应的元素设为6。因为在计算dfa的第j个状态时,只需要知道dfa是如何处理前j-1个字符的,所有总能从不完整的dfa中得到需要的信息。

1
void BuildDfa(char *pat, int dfa[][PATLENGTH]) {
2
    /* 初始化 */
3
    for (int i = 0; i < CHARLENGTH; i++) {
4
        for (int j = 0; j < PATLENGTH; j++) {
5
            dfa[i][j] = 0;
6
        }
7
    }
8
9
    dfa[pat[0]][0] = 1; /* 初始状态 */
10
11
    for (int X = 0, j = 1; j < PATLENGTH; j++) 
12
    {
13
        for (int c = 0; c < CHARLENGTH; c++) 
14
        {
15
            dfa[c][j] = dfa[c][x]; /* 匹配失败的情况 */
16
        }
17
        dfa[pat[j]][j] = j + 1; /* 匹配成功的情况 */
18
19
        X = dfa[pat[j]][X];  /* 更新重启位置X */
20
    }
21
}

基于PMT的KMP算法实现

转载整理至: 如何更好地理解和掌握 KMP 算法? - 海纳的回答 - 知乎

基于部分匹配表(Partial Match Table, PMT)的实现相对容易理解一些, 在说PMT之前,先说一下字符串的前缀与后缀。

  1. 字符串前缀集合: 如果字符串A和B, 存在A=BS,其中S是任意的非空字符串,那么称B为A的前缀,所有前缀的集合为该字符串的前缀集合。
  2. 字符串后缀集合: 如果字符串A和B, 存在A=SB,其中S是任意的非空字符串,那么称B为A的后缀,所有后缀的集合称为该字符串的后缀集合。

有了前缀和后缀的概念后则, PMT中的值的意义为: PMT中的每个值是当前字符串的前缀合集与后缀合集的交集中最长元素的长度。

例如:

  1. 单个字符’a’, 的前缀和后缀集合都为0, 则’a’的PMT值为0
  2. 字符串’ab’, 的前缀集合为{‘a’}, 后缀集合为{‘b’}, 前缀后缀集合不存在交集, 则’ab’的PMT值为0
  3. 字符串’aba’, 的前缀结合为{‘a’,’ab’}, 后缀集合为{‘ba’, ‘a’}, 交集为{‘a’}, 则’aba’的PMT值为1
  4. 同理’abab’, 前缀集合{‘a’,’ab’,’aba’}, 后缀集合为{‘bab’,’ab’,’b’}, 交集为{‘ab’}, PMT值为2
  5. ‘ababa’, 前缀集合为{‘a’,’ab’,’aba’,’abab’}, 后缀集合{‘baba’,’aba’,’ba’,’a’}, 交集为{‘a’,’aba’},则PMT值为3

所以对字符串"abababca",它的PMT表如下:

index 0 1 2 3 4 5 6 7
char: a b a b a b c a
PMT 0 0 1 2 3 4 0 1
next -1 0 0 1 2 3 4 0

由模式字符串的PMT的性质可知，主字符串中i指针之前的PMT[j −1]位就一定与模式字符串的第0位至第PMT[j−1]位是相同的。这是因为主字符串在i位失配，也就意味着主字符串从i−j到i这一段是与模式字符串的 0到j这一段是完全相同的。相同的这一段字符串的其前缀与后缀集合交集的最长元素长度为可省略比较的长度, 具体做法是: 保持i指针不动, 将j指针指向模式字符串的PMT[j-1]位即可。

构造next数组

next数组就是是将PMT数组向后偏移一位,将第0位的值设为-1,都是为了编程方便。

求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。具体来说就是:模式字符串的第一位(注意，不包括第0位)开始对自身(包括第0位)进行匹配运算。在任一位置，能匹配的最长长度就是当前位置的next值。

1
#include<stdio.h>
2
#include<string.h>
3
4
void getNext(char *t, int *next)
5
{
6
        int i = 0, j = -1;
7
        next[0] = -1;
8
9
        while(i < strlen(t))
10
        {
11
                if(j == -1 || t[i] == t[j])
12
                {
13
                        ++i;
14
                    ++j;
15
                        next[i] = j;
16
                }
17
                else
18
                        j = next[j];
19
        }
20
}
21
22
int KMP(char*s, char *t, int next[])
23
{
24
        int i = 0;
25
        int j = 0;
26
27
        while(i<(int)strlen(s) && j < (int)strlen(t))
28
        {
29
                if(j == -1 || s[i] == t[j])
30
                {
31
                        i++;
32
                        j++;
33
                }
34
                else
35
                        j = next[j];
36
        }
37
38
        if(j == strlen(t))
39
                return i - j;
40
        else 
41
                return -1;
42
43
}
44
void main()
45
{
46
        char *pat = "ABABAC";
47
        char *txt = "BCBAABACAABABACAA";
48
49
        int next[7];
50
51
        getNext(pat, next);
52
53
        printf("%d\n",KMP(txt, pat, next));
54
}