位图法(bitmap) & 布隆过滤器(Bloom Filter)

位图法就是利用位数组来存储数据状态，其优点就是节省数据存储空间。

布隆过滤器(Bloom Filter)是一种空间效率高的概率数据结构，由 Burton·Howar·Bloom 于1970年构思，用于测试元素是否是一组元素的成员。它实际上就是由一个很长的二进制向量(bitmap)和一系列随机映射函数(哈希函数)组成，将一系列数据通过一组哈希函数映射到位图数组中，以表示该数据存在。它的优点是空间效率和查询时间都远远超过一般的算法，缺点是有一定的误识别率和删除困难。

位图法(bitmap)

位图法就是利用位数组来存储数据状态，其优点就是节省数据存储空间。如下图所示：2 byte的位数组存储数字0,1,5,11。

15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	0

15	14	13	12	11	10	9	8	7	6	5	4	3	2	1	0
0	0	0	0	1	0	0	0	0	0	1	0	0	0	1	1

位运算

1	1 byte (字节)= 8 bit(位);
2	1 KB = 1024 B(字节);
3	1 MB = 1024 KB;
4	1 GB = 1024 MB;
5	1 TB = 1024 GB;


与(&)	0&0=0	1&0=0	0&1=0	1&1=1
或(\|)	0\|0=0	1\|0=1	0\|1=1	1\|1=1
异或(^)	0^0=0	1^0=1	0^1=1	1^1=0

左移运算

左移运算符m<<n表示把m左移n位。
在左移n位的时候，最左边的n位将被丢弃，同时在最右边补上n个0。

1	00001010<<2=00101000
2	10001010<<3=01010000

右移运算

右移运算符m>>n表示把m右移n位。

在右移n位的时候，最右边的n位将被丢弃。左边的处理情况分两种：

如果数字是一个无符号数值，则用0填补最左边的n位。
如果数字是一个有符号数值，则用数字的符号位填补最左边的n位。也就是说，如果数字原先是一个正数，则右移之后在最左边补n个0，如果数字原先是负数，则右移之后在最左边补n个1。

1	00001010>>2=00000010
2	10001010>>3=11110001

位图法实现

typedef char bitmap_type;
#define BITMAP_BITS (sizeof(bitmap_type)*8)
#define bitmap_set(b,v) (b[(v)/BITMAP_BITS] |= (1 << ((v)%BITMAP_BITS)))
#define bitmap_clear(b,v) (b[(v)/BITMAP_BITS] &= ~(1 << ((v)%BITMAP_BITS)))
#define bitmap_isset(b,v) (b[(v)/BITMAP_BITS] & (1 << ((v)%BITMAP_BITS)))
#define bitmap_zero(b) memset(b,0,sizeof(bitmap_type)*MAX_BUFFER_SIZE)

布隆过滤器

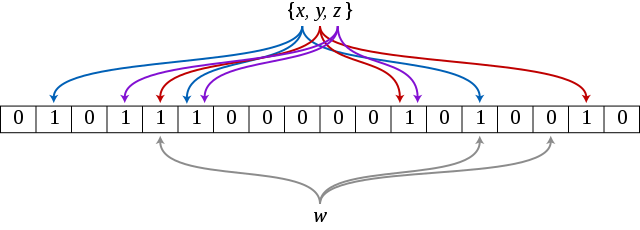
布隆过滤器比较常用的场景有:

网页url去重
垃圾邮件判别
数据库防止雪崩击穿
查询是否存在

False Positives

布隆过滤器器的误识别率(假正例False Positives)是指Bloom Filter认为某一元素存在于位集合中，但是实际上该元素不在集合中。

但是布隆过滤器器不存在识别错误(假反例False Negatives)的情况，即某个位元素不存在该位集合中，那么Bloom Filter不会判断该元素在集合中。

数学推导

假设：位数组大小为m，哈希函数个数为k，插入元素数量为n：

位数组中某一特定的位在进行元素插入后没有被插入的概率为：$1 - \frac{1}{m} $
在k次Hash操作后，该位置都没有被插入的概率为：$(1 - \frac{1}{m})^k$
插入n个元素后，某一位任然没有被插入的概率为：$(1-\frac{1}{m})^kn $
插入n个元素后，该位被插入的概率为：$1-(1-\frac{1}{m})^kn$

现在检测一个不在集合里的元素。经过哈希之后的这k个数组位置都是1的概率为：
$$(1-[1-\frac{1}{m}]^{kn})^k \approx (1-e^{-\frac{kn}{m}})^k $$

Hash最佳个数

对与给定的m和n，使误报率最小的k值为：$k=\frac{m}{n}\ln$ ，此时误报率为：$\ln p = -\frac{m}{n}(\ln 2)^2$ 。

bloom filter实现

typedef unsigned int (*hashfunc_t)(const char *);
typedef struct {
	size_t asize;
	unsigned char *a;
	size_t nfuncs;
	hashfunc_t *funcs;
} BLOOM;

#define SETBIT(a, n) (a[n/CHAR_BIT] |= (1<<(n%CHAR_BIT)))
#define GETBIT(a, n) (a[n/CHAR_BIT] & (1<<(n%CHAR_BIT)))

unsigned int sax_hash(const char *key)
{
	unsigned int h = 0;
	
	while(*key)
		h^=(h<<5)+(h>>2)+(unsigned char)*key++;

	return h;
}

unsigned int sdbm_hash(const char *key)
{
	unsigned int h = 0;
	
	while(*key)
		h=(unsigned char)*key++ + (h<<6) + (h<<16) - h;
	
	return h;
}

//bloom_create(2500000, 2, sax_hash, sdbm_hash);

BLOOM *bloom_create(size_t size, size_t nfuncs, ...)
{
	BLOOM *bloom;
	va_list l;
	int n;
	
	if(!(bloom=malloc(sizeof(BLOOM)))) return NULL;
	if(!(bloom->a=calloc((size+CHAR_BIT-1)/CHAR_BIT, sizeof(char)))) {
		free(bloom);
		return NULL;
	}
	if(!(bloom->funcs=(hashfunc_t*)malloc(nfuncs*sizeof(hashfunc_t)))) {
		free(bloom->a);
		free(bloom);
		return NULL;
	}

	va_start(l, nfuncs);
	for(n=0; n<nfuncs; ++n) {
		bloom->funcs[n]=va_arg(l, hashfunc_t);
	}
	va_end(l);

	bloom->nfuncs=nfuncs;
	bloom->asize=size;

	return bloom;
}

int bloom_destroy(BLOOM *bloom)
{
	free(bloom->a);
	free(bloom->funcs);
	free(bloom);

	return 0;
}

int bloom_add(BLOOM *bloom, const char *s)
{
	size_t n;

	for(n=0; n<bloom->nfuncs; ++n) {
		SETBIT(bloom->a, bloom->funcs[n](s)%bloom->asize);
	}

	return 0;
}

int bloom_check(BLOOM *bloom, const char *s)
{
	size_t n;

	for(n=0; n<bloom->nfuncs; ++n) {
		if(!(GETBIT(bloom->a, bloom->funcs[n](s)%bloom->asize))) return 0;
	}

	return 1;
}

1	typedef unsigned int (hashfunc_t)(const char );
2	typedef struct {
3	size_t asize;
4	unsigned char *a;
5	size_t nfuncs;
6	hashfunc_t *funcs;
7	} BLOOM;
8
9	#define SETBIT(a, n) (a[n/CHAR_BIT] \|= (1<<(n%CHAR_BIT)))
10	#define GETBIT(a, n) (a[n/CHAR_BIT] & (1<<(n%CHAR_BIT)))
11
12	unsigned int sax_hash(const char *key)
13	{
14	unsigned int h = 0;
15
16	while(*key)
17	h^=(h<<5)+(h>>2)+(unsigned char)*key++;
18
19	return h;
20	}
21
22	unsigned int sdbm_hash(const char *key)
23	{
24	unsigned int h = 0;
25
26	while(*key)
27	h=(unsigned char)*key++ + (h<<6) + (h<<16) - h;
28
29	return h;
30	}
31
32	//bloom_create(2500000, 2, sax_hash, sdbm_hash);
33
34	BLOOM *bloom_create(size_t size, size_t nfuncs, ...)
35	{
36	BLOOM *bloom;
37	va_list l;
38	int n;
39
40	if(!(bloom=malloc(sizeof(BLOOM)))) return NULL;
41	if(!(bloom->a=calloc((size+CHAR_BIT-1)/CHAR_BIT, sizeof(char)))) {
42	free(bloom);
43	return NULL;
44	}
45	if(!(bloom->funcs=(hashfunc_t)malloc(nfuncssizeof(hashfunc_t)))) {
46	free(bloom->a);
47	free(bloom);
48	return NULL;
49	}
50
51	va_start(l, nfuncs);
52	for(n=0; n<nfuncs; ++n) {
53	bloom->funcs[n]=va_arg(l, hashfunc_t);
54	}
55	va_end(l);
56
57	bloom->nfuncs=nfuncs;
58	bloom->asize=size;
59
60	return bloom;
61	}
62
63	int bloom_destroy(BLOOM *bloom)
64	{
65	free(bloom->a);
66	free(bloom->funcs);
67	free(bloom);
68
69	return 0;
70	}
71
72	int bloom_add(BLOOM bloom, const char s)
73	{
74	size_t n;
75
76	for(n=0; n<bloom->nfuncs; ++n) {
77	SETBIT(bloom->a, bloom->funcs[n](s)%bloom->asize);
78	}
79
80	return 0;
81	}
82
83	int bloom_check(BLOOM bloom, const char s)
84	{
85	size_t n;
86
87	for(n=0; n<bloom->nfuncs; ++n) {
88	if(!(GETBIT(bloom->a, bloom->funcs[n](s)%bloom->asize))) return 0;
89	}
90
91	return 1;
92	}

1	typedef char bitmap_type;
2	#define BITMAP_BITS (sizeof(bitmap_type)*8)
3	#define bitmap_set(b,v) (b[(v)/BITMAP_BITS] \|= (1 << ((v)%BITMAP_BITS)))
4	#define bitmap_clear(b,v) (b[(v)/BITMAP_BITS] &= ~(1 << ((v)%BITMAP_BITS)))
5	#define bitmap_isset(b,v) (b[(v)/BITMAP_BITS] & (1 << ((v)%BITMAP_BITS)))
6	#define bitmap_zero(b) memset(b,0,sizeof(bitmap_type)*MAX_BUFFER_SIZE)